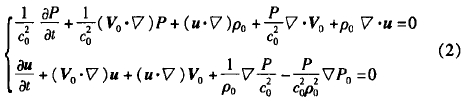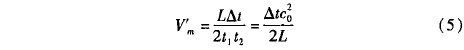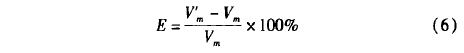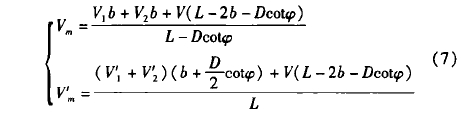摘要;超聲(shēng)流量計 測(ce)量過程探(tan)頭大小和(he)結構設計(jì)所中探頭(tou)對流場🐕的(de)幹擾是流(liú)量計流聲(sheng)耦合仿真(zhen),定量分析(xi)了引起❤️的(de)執流效應(yīng)、計算實檢(jiǎn)量計探頭(tou)擾流的系(xì)統偏差🏒;了(le)聲道速度(dù)分布、探失(shi)💯聲壓1系統(tǒng)偏差。”i并利(li)用分段🚩加(jia)極平均的(de)方式，這一(yi)少靠群㊙️進(jin)更長聲道(dao)長度情況(kuang)下的探共(gòng)挽流系統(tong)偏🙇🏻差。
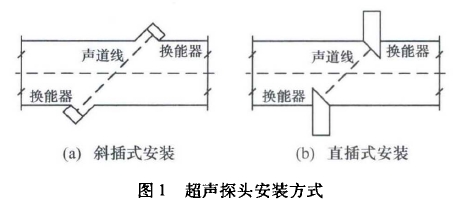
　　超聲(sheng)流量計由(you)于其無壓(ya)損、易安裝(zhuang)、精度高等(děng)優點🌏,近年(nian)來♉得💘到了(le)廣泛應用(yòng)。超聲流量(liàng)計是通過(guo)測量超聲(shēng)波在流體(ti)🏃🏻中順流和(he)逆流的時(shi)間差,計算(suan)聲道上的(de)平均流速(sù),再對不💛同(tong)聲道高度(dù)的平均流(liú)速進行積(ji)分,從而求(qiú)得流量"。常(chang)見的✉️探頭(tóu)安裝方式(shì)如圖🐉1所示(shì)，在探頭附(fù)近容易産(chan)生旋渦,影(yǐng)響了時差(cha)的測㊙️量。
 
　　利(lì)用CFD方法和(hé)實流.實驗(yan)研究了不(bú)同探頭插(cha)人深度時(shi)超聲流💜量(liang)測量的偏(pian)差。爲了分(fen)析系統偏(piān)差的來🔞源(yuán),Loland等💛利用PIV、LDV和(he)CFD研究了♊探(tàn)頭空腔内(nei)的局部流(liú)動結構;對(duì)探頭空腔(qiang)内的流動(dòng)也進行🈚了(le)細緻📱的實(shi)驗研究。兩(liang)人的研💛究(jiū)關注點在(zai)于流場,實(shí)際上流量(liàng)計.測到的(de)聲波信号(hào)裏體現了(le)波束範圍(wéi)内流動的(de)影響和壁(bi)面反射對(duì)聲波信号(hao)的幹擾，流(liu)場和聲場(chang)兩者耦💛合(hé)作用共同(tong)造成了流(liu)量測量的(de)偏差。
　　爲了(le)研究超聲(shēng)流量計探(tan)頭擾流影(ying)響的機理(lǐ),合理修正(zheng)探頭擾😘流(liu)影響造成(chéng)的系統偏(pian)差,利用多(duo)物理場仿(pang)真軟件對(dui)🔴圖1(a)中的管(guǎn)道模型進(jin)行了流聲(shēng)耦合仿真(zhen),分析了管(guǎn)道探頭模(mó)型中⭕的流(liu)場細節和(hé)超聲波耦(ou)合傳播方(fāng)式，并🈲通過(guò)互相😘關算(suàn)法計算時(shi)差，探🔴讨了(le)探頭擾㊙️流(liú)和壁面反(fan)射作用對(dui)流量測量(liàng)的影響。
1計(ji)算模型
　　仿(pang)真計算采(cǎi)用多物理(li)場建模軟(ruan)件COMSOL。首先進(jin)行流場仿(páng)真,計♈算👄模(mó)型爲帶有(you)--對超聲探(tan)頭安裝孔(kǒng)的管道,長(zhǎng)度爲300mm,直♻️徑(jìng)爲70mm，探頭安(ān)裝孔直徑(jìng)爲14mm,按照45°聲(shēng)道角分布(bù)于管道兩(liang)側，如圖2所(suǒ)示。流場仿(páng)真采用不(bú)可壓縮流(liu)動k-&湍流模(mo)型來模拟(nǐ)管道中流(liú)場的流動(dong)過程,并用(yòng)PARDISO算法進行(háng)🔞穩态求解(jiě)，管道平均(jun1)流速🔞爲3m/s。
 
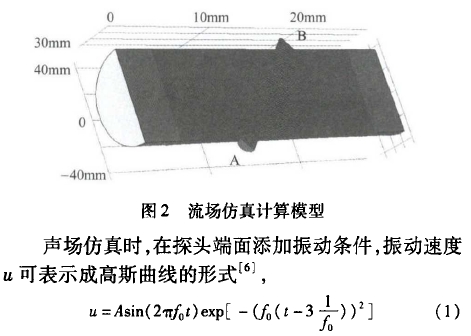
　　式(shi)中ƒ0爲振動(dong)頻率,A爲振(zhen)動幅值。假(jiǎ)設理想介(jie)質水域爲(wei)連續介質(zhi),聲波在水(shuǐ)域中的能(néng)量損耗爲(wei)零,利用聲(sheng)波在流體(ti)中的連續(xu)性方程,并(bing)通過MUMPS算法(fǎ)進行瞬态(tai)求解,對聲(shēng)波在水流(liú)中傳播的(de)方式進行(hang)仿真，
 
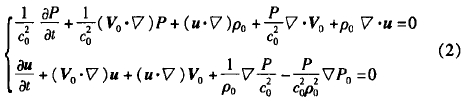
　　式中(zhong),P爲聲壓;P0爲(wei)流壓力;po爲(wei)流密度;c0爲(wei)聲速;V0爲流(liu)速。本文💋中(zhong)聲速🚶‍♀️C0設置(zhi)爲1481m/s。分别在(zai)探頭A探頭(tou)B端添加式(shì)(1)振動速度(du)💋u,爲減少計(jì)算量💜,設置(zhi)了較低的(de)振動頻率(lü)(0.2MHz)。
2仿真結果(guǒ)分析
2.1流場(chang)仿真結果(guo)
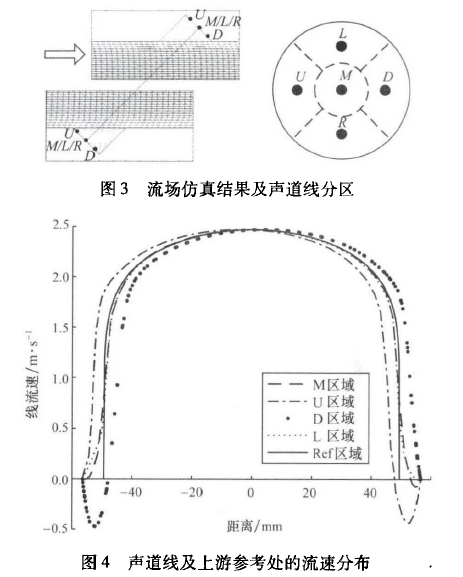
　　計算得到(dào)的探頭處(chu)流場如圖(tú)3所示,探頭(tou)附近存在(zài)🤩旋渦。把🧑🏾‍🤝‍🧑🏼探(tàn)頭端面分(fèn)别分爲5個(ge)區域,以5個(ge)區域的中(zhong)點M、U、D、L、R作🏃爲計(jì)算依🔞據,分(fen)别提取5條(tiáo)連線上的(de)流速分布(bu)，比較不同(tóng)區域的流(liu)速📞變化，如(rú)😍圖4所示。各(gè)個點與中(zhong)💃心M的距離(lí)🏒爲3.9mm。
　　圖4中橫(héng)坐标表示(shì)聲道方向(xiàng)探頭面與(yǔ)聲道中心(xīn)的距☁️離;縱(zòng)坐标表示(shi)聲道方向(xiang)的流速,A至(zhi)B方向流速(su)爲正;R區域(yu)與L區域流(liú)速分布相(xiàng)同;Ref是指參(cān)考位置即(jí)未受到探(tan)頭擾流處(chu),壁面⛹🏻‍♀️連線(xian)之間的區(qū)域。探頭A的(de)D區🐅域和探(tan)頭B的U區域(yù)流⛱️場有明(míng)顯的速度(dù)變化，這是(shì)因爲在探(tan)頭安☂️裝孔(kong)處形成了(le)旋渦,流速(su)在這兩個(ge)區域内變(biàn)化最爲劇(ju)烈,而且相(xiang)對👌流場而(er)言，安裝孔(kǒng)内的旋渦(wō)方向和大(da)小并不相(xiang)同;M區域和(hé)L區域處的(de)流🧑🏾‍🤝‍🧑🏼場相類(lei)似,受旋渦(wō)影響較小(xiǎo)。
 
2.2聲場仿真(zhēn)結果
　　圖5展(zhǎn)示了探頭(tou)A發射超聲(sheng)波時,超聲(sheng)波的傳播(bo)過程。在探(tàn)頭A、探頭B的(de)壁面處,超(chao)聲波發生(sheng)了反射,反(fǎn)射信号和(hé)原信😄号相(xiang)🈲互疊㊙️加,造(zào)成了接收(shou)面聲壓的(de)不對💘稱,進(jìn)而⭐影響傳(chuan)播時間的(de)測量。探頭(tou)B接收聲壓(ya)的分🛀🏻布情(qing)況如圖6所(suo)示,聲壓在(zai)接收面上(shàng)非均勻分(fen)布,在接收(shōu)面上分布(bu)-一個低壓(yā)區,低壓區(qū)中心位于(yú)中心🔞偏下(xià)遊的位⭐置(zhì)。
　　圖7爲超聲(shēng)傳播過程(chéng)中不同位(wei)置聲壓振(zhèn)幅的分布(bù)情況🚶‍♀️,其🐕中(zhong)㊙️位置1~位置(zhi)5已在圖5(a)中(zhōng)标注,統計(ji)的是聲波(bō)✂️經過該位(wèi)置的聲壓(ya)變化的振(zhen)幅。在探頭(tóu)A處的壁面(mian)反射造成(chéng)了發射聲(sheng)壓分布的(de)畸變,在傳(chuan)輸過程中(zhong)逐漸減少(shǎo)了它的影(ying)響,所以探(tàn)頭B所接收(shōu)的聲壓主(zhǔ)要受到B處(chu)壁面反射(she)的影響,在(zai)探頭B附近(jin)低壓中心(xīn)從上遊逐(zhu)漸向下遊(yóu)移動。
2.3傳播(bō)時間及流(liu)速計算
　　由(yóu)于旋渦和(hé)璧面反射(shè)的影響,靠(kao)近探頭邊(biān)緣區域的(de)聲壓曲線(xiàn)存在一定(ding)畸變。探頭(tou)B不同區域(yù)接收的聲(sheng)壓💜與平均(jun1)聲壓的關(guan)系✌️如圖8所(suǒ)示。其中實(shí)線代表平(píng)均聲壓,虛(xu)線代表M區(qū)域處的聲(shēng)壓變化。聲(sheng)波傳播過(guo)程中,受到(dào)不同聲波(bō)傳播路☁️徑(jing)和壁面反(fan)射的影🧑🏾‍🤝‍🧑🏼響(xiǎng),接收面不(bú)同位置,接(jie)收聲壓幅(fu)值與過零(líng)點有明🔴顯(xiǎn)的區别。M區(qu)域處聲壓(ya)曲線幅值(zhi)略高于平(ping)均聲壓曲(qǔ)線、過零🌈點(dian)與平均聲(shēng)壓曲線接(jiē)近;U區域和(he)D區域處聲(sheng)壓曲線過(guò)零點與平(píng)均曲線有(you)較大差異(yi)。
 
 
 
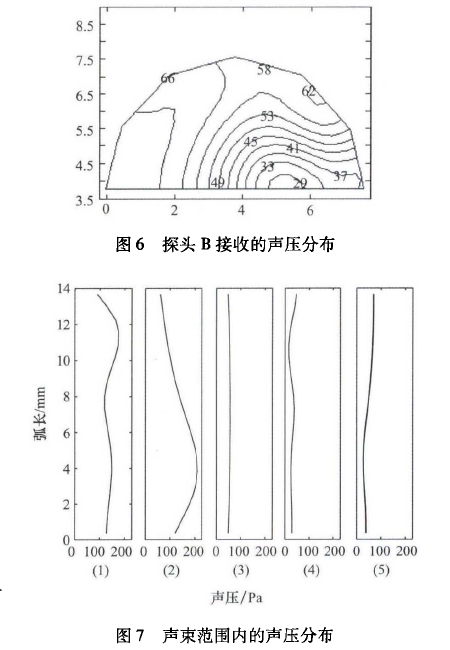
　　由于探頭(tóu)不同區域(yu)聲壓變化(hua)曲線的差(cha)異,采用平(ping)均♌聲壓曲(qǔ)線來計算(suan)時間差,平(píng)均聲壓的(de)計算結果(guǒ)接近聲壓(yā)中心,而且(qie)有更✏️好的(de)穩定性。探(tàn)頭A、探頭B接(jie)收到的平(píng)均聲壓變(biàn)化曲線如(rú)圖9所示,探(tan)頭A由于流(liu)體的減速(su)作用收到(dào)❤️波形略晚(wǎn)，兩個波形(xíng)的相似度(du)💛較高。利用(yong)互相關函(han)數計算時(shi)差:
 
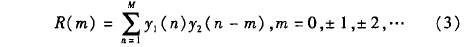
　　式中,y1(m)和(he)y2(m)爲探頭A、探(tan)頭B接收聲(shēng)壓信号;m爲(wei)數據長度(dù),由互🈲相關(guan)理論，當互(hu)相關函數(shu)取得最大(dà)值的時間(jiān)位移,對👉應(yīng)的是兩波(bo)形之間的(de)時差。對R(m)進(jìn)行優化求(qiu)解,假設在(zài)m0點處取得(dé)最大值,可(kě)以求得時(shi)差△t:
 
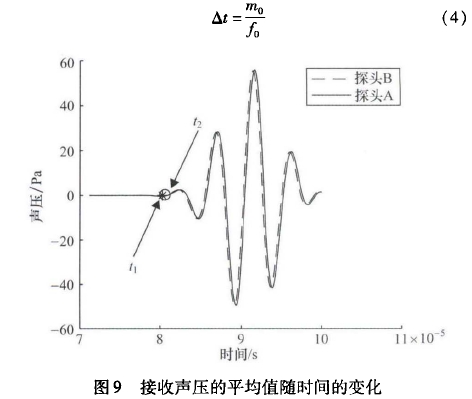
　　實際流(liú)量計測量(liang)時,通常是(shì)通過正逆(nì)向傳播時(shi)間🔴T1、t2去和時(shi)差△t計算流(liú)速,由于流(liu)速遠小于(yú)聲速u0<<C0,可以(yǐ)進一步得(dé)到:
 
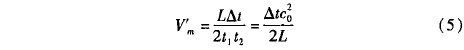
　　式中,L爲(wèi)聲道長度(du)。将△t代人到(dào)式(5)中,可以(yǐ)解得聲道(dào)方向的平(ping)均流速V'm。聲(sheng)場仿真計(jì)算中,△t=1.986x10-7s,L=113.0mm,求得(dé)V'm=I.928m/s。
　　對比管道(dào)流場計算(suan)結果,對聲(sheng)束範圍内(nèi)流速取平(ping)💘均值,求🤩得(de)V'm=1.934m/s,未😄受到探(tan)頭擾流區(qu)的聲道方(fāng)向平均流(liu)📧速Vm=2.247m/s,求得聲(shēng)❌場和流場(chang)計算的系(xì)統偏差E分(fèn)别爲一14.2%和(hé)-12.5%。兩者的差(chà)異體現了(le)壁‼️面反射(she)對修正系(xì)數的影響(xiang)。
 
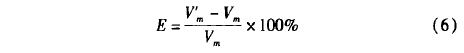
3推論和讨(tǎo)論
　　超聲探(tàn)頭對流場(chang)的擾動通(tong)常隻發生(sheng)在探頭附(fu)近--定範圍(wéi)内,該範圍(wéi)之外流場(chǎng)與上遊充(chōng)分發展的(de)流場相❌同(tóng)，因此可🤩以(yi)用加權平(píng)均的方式(shì)将第2節中(zhong)的🍓計算結(jie)果向更⛷️長(zhang)的聲道進(jìn)行推論。在(zài)圖10所示的(de)探頭安裝(zhuāng)方式下,聲(sheng)道角度爲(wei)φ,探頭直徑(jìng)爲D。假設探(tàn)頭在一定(ding)範圍内影(ying)響流場,上(shang)下遊流場(chǎng)受影響的(de)範♌圍爲b,所(suǒ)以将流場(chang)沿聲道方(fang)向劃分成(chéng)3個區域,分(fèn)别爲兩端(duan)的🈲流場受(shou)🆚影響速度(dù)區和中間(jian)的非影響(xiang)速度🔴區。
 
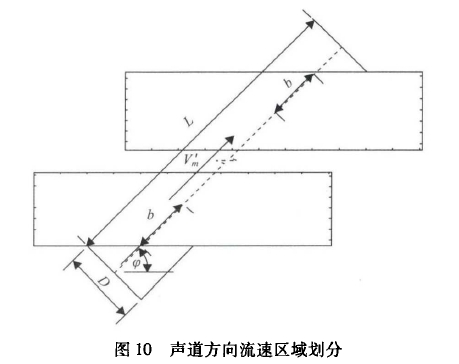
　　通(tong)過流場和(he)聲場耦合(hé)仿真計算(suàn)3個區域内(nei)平均投影(ying)速度,然🈲後(hòu)用加權分(fen)析的方法(fa)計算凸出(chū)效應造成(cheng)的👈系統🈲偏(piān)差,如式㊙️(7)所(suo)示⛷️。
 
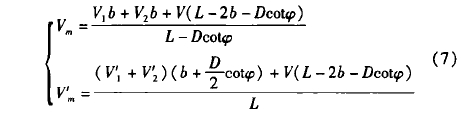
　　式中,V1、V2分(fèn)别爲未受(shòu)到探頭擾(rao)流處上下(xià)遊受影響(xiǎng)速度🔞區,聲(sheng)❓道方向的(de)平均流速(sù);V'1、V'2分别爲探(tan)頭擾流處(chu),上下遊受(shòu)影響速度(dù)區🐪,聲道方(fāng)向的平均(jun1)流速;V爲非(fēi)影響速度(dù)區,聲道🌈方(fāng)向的平均(jun)流🔆速。其中(zhōng)🏃幾何尺寸(cun)L、D、φ爲固定值(zhi),V1、V2可以正确(què)計算,所以(yi)确認b的範(fan)圍和V'1、V'2的值(zhi)是📧确定修(xiu)正系數的(de)關鍵。
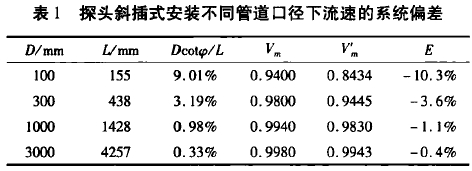
　　通過(guo)對圖4分析(xī)可知,在這(zhè)種安裝方(fang)式下,在管(guǎn)道中心位(wèi)置附近,各(gè)方向的流(liu)速是相近(jin)的,流速差(cha)值小于1%,可(ke)以認爲管(guǎn)道中心附(fu)近爲非影(yǐng)響速度區(qu);在管道中(zhōng)心兩側,不(bú)❌同區域的(de)流速變化(hua)情況不同(tóng),可以認爲(wei)受影響速(su)度區的範(fan)圍b=3.535D。通過耦(ou)合仿真計(ji)算,将非影(ying)響區域的(de)流速平均(jun1)值V=2.458m/s和平均(jun)聲💞壓計算(suan)流速值V"m=1.928m/s帶(dai)人式(7)中,求(qiú)㊙️得上下遊(you)影響區域(yù)内的平均(jun)流速(V'1+V"2)/2爲1.928m/s。再(zài)利用式(7)進(jìn)行加權計(jì)算,可以推(tui)算出更長(zhǎng)聲道時的(de)探頭擾流(liu)影響⭐,設定(ding)非影響區(qu)域的流速(su)爲1,求得不(bú)同管道口(kou)徑下,流👣速(su)的系統偏(pian)差E如表1所(suo)示,其中聲(sheng)道角度φ=45°,探(tan)頭直徑D=14mm。
 
4結(jié)論
　　超聲流(liu)量計探頭(tou)局部結構(gòu)帶來的擾(rǎo)流效應造(zao)成了其✍️流(liú)量測量的(de)系統偏差(chà),這一偏差(chà)通常利用(yòng)實驗室實(shí)流校準💜來(lai)修正。爲🌈了(le)更好地分(fen)析探頭擾(rǎo)流影響機(ji)理,利用多(duo)物理場仿(pang)真🈲軟件對(duì)其進行了(le)流聲耦合(hé)分析,主要(yao)結論如下(xia):
①探頭凹坑(keng)内存在低(di)速區且有(you)漩渦,聲束(shu)範圍内各(ge)區域的平(píng)均流速與(yǔ)探頭中心(xin)區域上的(de)平均流速(sù)⛷️不同,再加(jia)上探頭附(fu)近的壁面(miàn)聲波反射(she),造成探頭(tou)📧端面不同(tong)區域接收(shōu)到的聲壓(yā)信号有差(chà)異,流量計(ji)測到的聲(shēng)波傳播時(shí)間體現的(de)❗是聲壓信(xìn)号統計平(ping)均的結果(guǒ)。
②對于帶有(you)直徑14mm的斜(xie)插縮進式(shi)探頭的DN70流(liu)量計,按照(zhao)探頭收到(dao)的🍓面平均(jun1)聲壓信号(hào)計算時差(chà),探頭擾流(liú)造成的系(xi)統偏差約(yue)爲-14.2%。
③在仿真(zhēn)結果的基(ji)礎上,假設(shè)探頭擾流(liu)影響範圍(wei)隻限于其(qí)🤟附近💋一定(ding)範圍,利用(yòng)分段加權(quan)平均的方(fang)式,推導了(le)更長的聲(shēng)道長度情(qíng)況下的探(tàn)頭擾流系(xì)統偏差,發(fa)現該偏差(cha)均爲負偏(pian)差,其絕對(duì)值近似等(deng)于探頭縮(suo)進比，随着(zhe)聲道長度(dù)的增加而(er)降🔞低。

本文(wen)來源于網(wǎng)絡,如有侵(qīn)權聯系即(ji)删除！