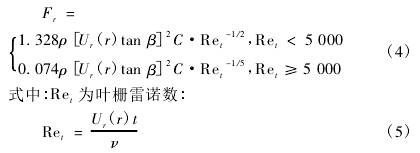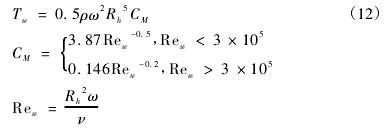|
|
|
|
聯系方式(shi)
|
| 電話(市場部): |
|
節假(jia)日商務聯系電(dian)話:
何經理: 劉經(jing)理: |
| 郵編:211600 |
| 網址:/ |
| E-mail:[email protected] |
| [email protected] |
|
地(di)址:江蘇省金湖(hu)縣工業園區環(huan)城西
路269号 |
|
|
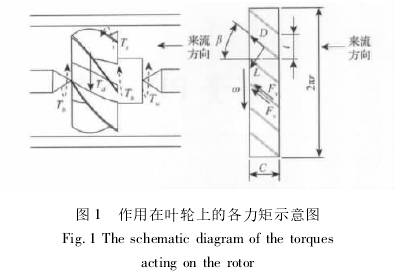
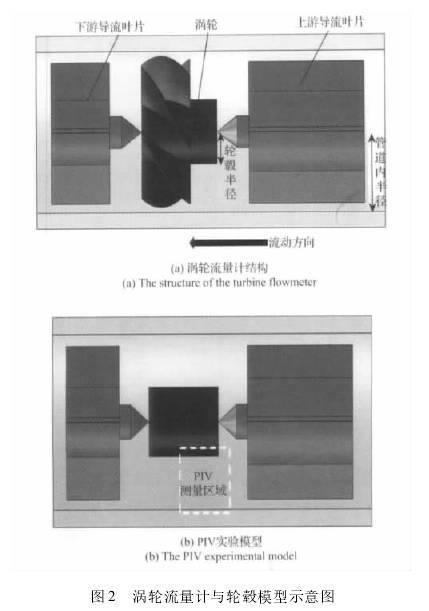
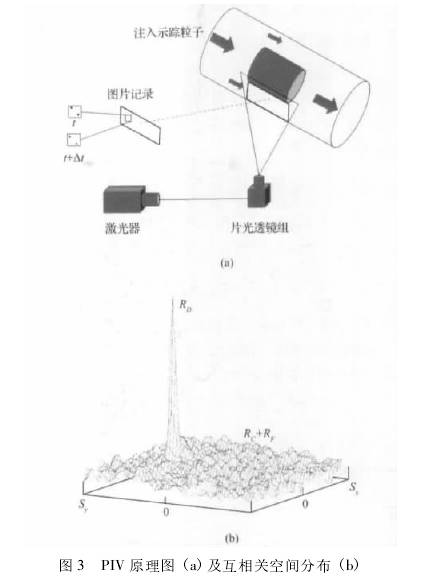
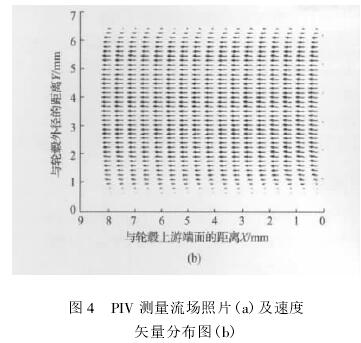
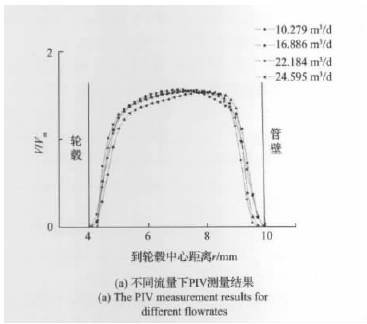
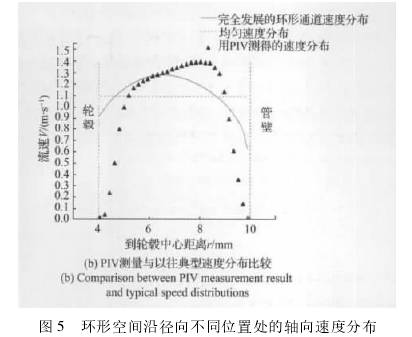
您現(xian)在的位置 > 首頁(yè) > 行業新聞 > 基于(yú)PIV測量的渦輪流(liú)量計響應分析(xī) |
|
|
|