1引 言(yan)
    工業生(sheng)産過程(cheng)參數如(ru)溫度,壓(ya)力等檢(jian)測中以(yi)流量和(he)各🌈相持(chi)率㊙️測量(liang)複雜是(shi)較難測(ce)量的兩(liang)個參數(shu)。因而引(yin)✉️起了工(gong)程技術(shu)人員的(de)興趣。随(sui)着工業(ye)的發展(zhan)被測對(dui)象不再(zai)限于單(dan)相而要(yao)對多相(xiang)流,混合(he)狀态的(de)流量進(jin)行測量(liang)-測量多(duo)相流的(de)技術難(nan)💃🏻度要比(bi)單相流(liu)體的正(zheng)♋确測量(liang)大得多(duo)知道單(dan)相流體(ti)的密度(du)⛹🏻‍♀️,粘度及(ji)測量裝(zhuang)置的幾(ji)何結構(gou) 便可以(yi)對單相(xiang)流進行(hang)定量分(fen)析。如果(guo)能利用(yong)♉多相流(liu)中每一(yi)相的上(shang)述各物(wu)理量對(dui)多相流(liu)進行測(ce)量得話(hua)就很方(fang)便，-但遺(yi)憾的是(shi)多相流(liu)體的特(te)性遠比(bi)單相流(liu)體的特(te)性複雜(za)得多如(ru)各組分(fen)✉️之間不(bu)能均勻(yun)混合,混(hun)合流體(ti)的異常(chang)性,流型(xing)轉變相(xiang)對速度(du),流體性(xing)質,管道(dao)結構,流(liu)⁉️動方向(xiang)等因素(su)将導緻(zhi)渦輪流(liu)量傳感(gan)器響應(ying)特性♋的(de)改變.
    渦(wo)輪流量(liang)傳感器(qi) 和顯示(shi)儀表組(zu)成的液(ye)體渦輪(lun)流量計(ji)以良好(hao)的重複(fu)❗性,寬🌈廣(guang)的線性(xing)工作區(qu)和精度(du)高而受(shou)到用戶(hu)的歡迎(ying).液體🐇渦(wo)輪流量(liang)計在測(ce)量單相(xiang)時工作(zuo)穩定性(xing)🙇🏻較 好但(dan)在多相(xiang)流動時(shi)由于各(ge)相的速(su)㊙️度,粘度(du),局部持(chi)率等因(yin)素影響(xiang)渦輪轉(zhuan)速-按常(chang)規同一(yi)流量所(suo)對應的(de)渦輪轉(zhuan)速保持(chi)不變即(ji)儀器常(chang)數不變(bian)-但在多(duo)✉️相流動(dong)時即使(shi)在總流(liu)量保持(chi)不變的(de)情況下(xia)♌混合流(liu)體的密(mi)度發生(sheng)變化也(ye)🙇‍♀️會引起(qi)渦輪轉(zhuan)速的很(hen)大變化(hua)-由于在(zai)多相流(liu)動中渦(wo)輪響應(ying)特性發(fa)生了變(bian)化目前(qian)面臨的(de)問題是(shi)渦輪流(liu)量傳感(gan)器是否(fou)能成功(gong)地應用(yong)于多相(xiang)流的測(ce)量及如(ru)何設計(ji)用于多(duo)相流測(ce)量的渦(wo)輪流量(liang)傳感器(qi)-就此問(wen)題 這裏(li)首先對(dui)渦輪傳(chuan)感器進(jin)行了理(li)論🈲分析(xi)然🙇🏻後給(gei)出三相(xiang)流動中(zhong)液體渦(wo)輪流量(liang)計的實(shi)驗響應(ying)特性最(zui)⭕後總結(jie)出用液(ye)體渦輪(lun)流量計(ji)測量多(duo)相流流(liu)量的半(ban)理論半(ban)經驗公(gong)式
2.液體(ti)渦輪流(liu)量計測(ce)量原理(li)
2.1流量計(ji)的響應(ying)方程
    液(ye)體渦輪(lun)流量計(ji) 通過渦(wo)輪轉數(shu)反映被(bei)測流量(liang)的大小(xiao)渦輪轉(zhuan)數N與🔞流(liu)量Q之💁間(jian)的關系(xi)可以表(biao)示爲N=K(Q-q)
式(shi)中:K-儀表(biao)常數
q-啓(qi)動流量(liang)通過标(biao)定獲得(de)
2.2液體渦(wo)輪流量(liang)計固有(you)儀表常(chang)數的理(li)論計算(suan)
液體渦(wo)輪流量(liang)計固有(you)儀表常(chang)數K0主要(yao)與渦輪(lun)傳感器(qi) 結構參(can)數有關(guan) 圖(1), K0可按(an)下式計(ji)算


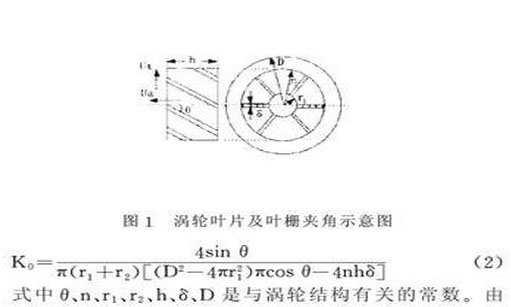
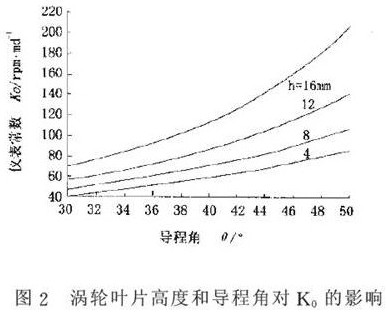
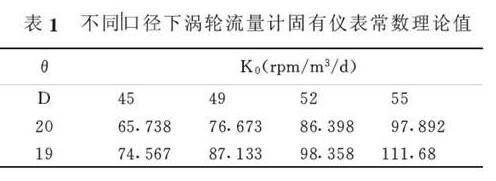
    式2可(ke)見,對确(que)定的渦(wo)輪流量(liang)傳感器(qi))易知口(kou)徑D大, K0值(zhi)‼️小,葉片(pian)數❤️n大, K0值(zhi)大等.如(ru)果要獲(huo)得較大(da)的儀表(biao)常數,就(jiu)要對渦(wo)輪傳✊感(gan)器的結(jie)構參數(shu)進行優(you)化設計(ji),從💚圖2(可(ke)以♌看出(chu),葉片高(gao)度;增加(jia), K0增大,導(dao)程角增(zeng)大, K0增大(da)♋.對于￠19的(de)過環空(kong)大排量(liang)液體渦(wo)輪流量(liang)計而言(yan),由上式(shi)計算得(de)K0=74.567rpm/m3/d而水中(zhong)标定的(de)🐉KW=78.89rpm/m3/d,表1給出(chu)不同口(kou)徑和不(bu)同導程(cheng)角下液(ye)體渦輪(lun)流量計(ji)固有儀(yi)表常數(shu)的計算(suan)🌈值.

3.液體(ti)渦輪流(liu)量計在(zai)多相流(liu)中的響(xiang)應實驗(yan)
    實驗在(zai)以空氣(qi)、柴油和(he)水爲介(jie)質的三(san)相流動(dong)模拟♍裝(zhuang)置中進(jin)行，透明(ming)的井筒(tong)内徑爲(wei)125mm流體全(quan)部集流(liu)後進入(ru)流量計(ji),實㊙️驗發(fa)現,總流(liu)量相等(deng),但流動(dong)密度不(bu)等的實(shi)📧驗, K0值變(bian)化較大(da);流動密(mi)度相等(deng),總流量(liang)不等🈚的(de)實驗, K0值(zhi)變化較(jiao)小⛱️圖(3).多(duo)相流動(dong)中渦輪(lun)儀器常(chang)數校正(zheng)因子CK與(yu)流動密(mi)度Pn之間(jian)的統計(ji)關系爲(wei)CK=Pn 0.5次方

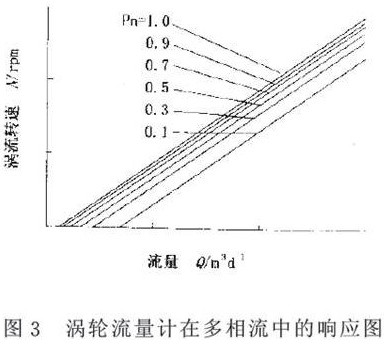
4．多(duo)相流流(liu)量測量(liang)
    由于機(ji)械加工(gong)及安裝(zhuang)工藝等(deng)方面的(de)原因，按(an)液體🥰渦(wo)⭕輪流❤️量(liang)📞計固有(you)儀表常(chang)數設計(ji)的渦輪(lun)，必須在(zai)水中标(biao)定後🤞才(cai)能使用(yong)，設水♉中(zhong)标定的(de)渦輪儀(yi)表常數(shu)爲kw則通(tong)過上述(shu)理論計(ji)算和實(shi)😘驗,歸納(na)總結出(chu)液體♍渦(wo)輪流量(liang)計在多(duo)相流動(dong)中的😍響(xiang)應方程(cheng)爲:
Q=N/K+q
K=KW+K0(Pn 0.5次方(fang)-1_
式中kVV爲(wei)水中标(biao)定的儀(yi)表常數(shu)
    如果用(yong)全集流(liu)型液體(ti)渦輪流(liu)量計測(ce)得渦輪(lun)轉數N,在(zai)标準計(ji)量裝置(zhi)上通過(guo)标定獲(huo)得kw和q結(jie)合輔助(zhu)參數Pn就(jiu)可以用(yong)公式(3)計(ji)算出❄️多(duo)相流總(zong)量.用(3)式(shi)在油井(jing)的油、氣(qi)、水多相(xiang)流流量(liang)測量中(zhong)得到了(le)實際應(ying)用，計算(suan)誤差在(zai)5%以内。
5.結(jie)論
    通過(guo)理論計(ji)算和多(duo)相流實(shi)驗)總結(jie)出了液(ye)體渦輪(lun)流量☁️計(ji)儀器常(chang)數在多(duo)相流動(dong)中的實(shi)驗關系(xi))結合理(li)論和實(shi)驗)給出(chu)了用液(ye)體渦輪(lun)流量計(ji)測量多(duo)相流總(zong)流量的(de)半經驗(yan)半理論(lun)關系式(shi))實際應(ying)用證明(ming)該方法(fa)可行。