摘(zhai)要:傳統電(dian)磁流量計(ji) 采用硬件(jian)濾波方式(shi)去除噪聲(sheng),但由于采(cai)用硬件濾(lü)💃🏻波消🏃‍♂️噪的(de)能力與器(qi)件的動态(tai)調節相互(hu)矛盾,且硬(ying)件電路元(yuan)🌈件的非理(li)想化必然(ran)會混入其(qi)他噪聲.爲(wei)🈲了彌補硬(ying)件濾波的(de)缺點，采用(yong)了軟件去(qu)噪算法，該(gai)算法基于(yu)小波消噪(zao)原理.爲有(you)效去除電(dian)磁流量計(ji)🔴輸出信号(hao)中的幹擾(rao)信号，提高(gao)數據處理(li)的穩定性(xing)👣和數據的(de)精度,在結(jie)合傳統軟(ruan)、硬阈值函(han)數的不足(zu)的基礎上(shang),引入了一(yi)種新阈值(zhi)函數,且在(zai)傳統信噪(zao)比、均方誤(wu)差等單一(yi)評價标準(zhun)的基礎上(shang)引入了一(yi)種綜合評(ping)價标準對(dui)去噪效果(guo)進行評估(gu),采用MATLAB工具(ju)箱對去噪(zao)結果進行(hang)了仿🚩真.結(jie)果表明，相(xiang)比傳統小(xiao)波消噪方(fang)法，改進的(de)小波阈值(zhi)去噪方法(fa)對抑制電(dian)㊙️磁流量計(ji)信号中的(de)各種🏃噪聲(sheng)幹擾有更(geng)好效果.
　　電(dian)磁流量計(ji)是一種基(ji)于法拉第(di)電磁感應(ying)定律來測(ce)量管内導(dao)電介質體(ti)積流量的(de)感應式儀(yi)表,它輸出(chu)的微弱信(xin)号常被複(fu)雜的幹擾(rao)所覆蓋.傳(chuan)統信号處(chu)理電路配(pei)置硬件濾(lü)波器來濾(lü)除流量信(xin)号中的🥵高(gao)頻幹擾,但(dan)硬件電路(lu)存在元件(jian)的非理想(xiang)化會引人(ren)其他噪聲(sheng)和不能動(dong)态調節兩(liang)個弊端.
　　針(zhen)對硬件電(dian)路的不足(zu)引人了小(xiao)波變換和(he)MATLAB相結合的(de)去噪算法(fa).相比于傳(chuan)統傅裏葉(ye)變換,小波(bo)變換在去(qu)除掉高頻(pin)噪🌈聲的同(tong)時保留了(le)信号的高(gao)頻成分,其(qi)分辨率分(fen)析具有良(liang)好的時頻(pin)特性.國内(nei)外學者們(men)針對電磁(ci)流量計信(xin)号,提出了(le)不同的🔆去(qu)噪方法對(dui)其進行處(chu)理分析.用(yong)Haar 小👌波對染(ran)噪信♈号進(jin)行不同尺(chi)度的濾波(bo),可以得到(dao)較好的去(qu)噪效果0-2;通(tong)過對漿液(ye)噪聲的🚶分(fen)析建模确(que)立❗電磁流(liu)量計克服(fu)漿液噪聲(sheng)❄️的有效方(fang)案,對漿液(ye)測量有促(cu)進作用。本(ben)研究引入(ru)一種改進(jin)的新阈值(zhi)函數對電(dian)磁流量計(ji)輸出的傳(chuan)感信号進(jin)行去噪處(chu)理,經實驗(yan)仿真表明(ming),這種方🐉法(fa)對電磁流(liu)量計數據(ju)降噪效果(guo)顯著,爲提(ti)取較爲純(chun)淨的電磁(ci)流量計信(xin)号提供🛀🏻了(le)參考.
1電磁(ci)流量計信(xin)号及其噪(zao)聲特征分(fen)析
　　電磁流(liu)量計在其(qi)使用過程(cheng)中會受到(dao)各個方面(mian)的幹♋擾産(chan)生各種噪(zao)聲,具體噪(zao)聲模型如(ru)下:
 
ec爲工頻(pin)幹擾,ed爲電(dian)化學幹擾(rao).
　　在衆多噪(zao)聲中,工頻(pin)幹擾通過(guo)采集數據(ju)對相位的(de)選取可以(yi)消💘除,微分(fen)幹擾隻出(chu)現在勵磁(ci)變化處，當(dang)勵磁不變(bian)時,不存在(zai)微分幹擾(rao).低頻同相(xiang)幹擾可以(yi)忽略不計(ji).電化學幹(gan)擾頻帶很(hen)寬,在低頻(pin)和高頻都(dou)有.
2電磁流(liu)量計信号(hao)去噪算法(fa)模型
2.1小波(bo)變換阈值(zhi)降噪方法(fa)基本原理(li)
　　傳統的硬(ying)閡值函數(shu)去噪方法(fa)和軟阈值(zhi)函數去噪(zao)方法,其應(ying)用也極廣(guang),但不可忽(hu)視其缺點(dian).
1)硬阈值函(han)數
 
　　硬阈值(zhi)算法由于(yu)自身不連(lian)續的缺點(dian),在去噪時(shi)産生“僞吉(ji)布斯現象(xiang)”,丢失了許(xu)多原始信(xin)息.
2)軟阈值(zhi)函數
 
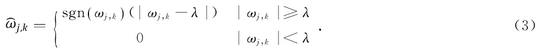
　　軟阈(yu)值處理後(hou)的小波系(xi)數與理論(lun)的小波系(xi)數存在固(gu)😍定誤差,容(rong)易造成高(gao)頻有用信(xin)息的遺失(shi).
2.2新型小波(bo)降噪方法(fa)阈值函數(shu)及阈值選(xuan)取
　　許多學(xue)者對軟、硬(ying)阈值函數(shu)采用改進(jin)算法.但這(zhe)些阈值函(han)數都🐉是基(ji)于傳統的(de)阈值函數(shu),仍然存在(zai)平滑度低(di)且高階不(bu)可導的不(bu)足.針對這(zhe)些阈值函(han)數的不足(zu),本文選取(qu)了一種含(han)有不同未(wei)知數的阈(yu)值函數,該(gai)阈值函數(shu)不僅介于(yu)軟、硬阈值(zhi)函數中間(jian),同☁️時集成(cheng)了它們的(de)優點,且添(tian)加了平滑(hua)過渡區.以(yi)此來解決(jue)傳統兩種(zhong)阈值函數(shu)的不足.引(yin)人的新阈(yu)值函數如(ru)下🌐:
 
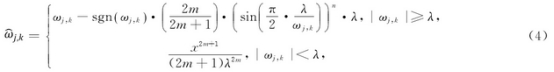
　　式中參(can)數m和n均爲(wei)正數,是公(gong)式中的調(diao)節因子,其(qi)用作調節(jie)幅值,可以(yi)針對不同(tong)含噪信号(hao),使閡值函(han)數曲線可(ke)以提取去(qu)噪效果更(geng)好的信号(hao).采用2m .2m+1諸如(ru)此類的調(diao)節參數,其(qi)目的是得(de)到一個在(zai)阈值處平(ping)滑過渡的(de)區域,在這(zhe)個區域内(nei)有用信号(hao)的成分會(hui)被有效的(de)保存，避免(mian)被當成噪(zao)聲而濾除(chu)掉.同時,采(cai)用和這樣(yang)的系數保(bao)證了阈值(zhi)函數在閥(fa)值處的不(bu)間斷.新阈(yu)值㊙️函數在(zai)小于閥值(zhi)區間内,漸(jian)進最後趨(qu)于0的曲線(xian),此曲線接(jie)近于0但不(bu)等于0.
2.3小波(bo)分解最佳(jia)尺度和小(xiao)波基
2.3.1 分解(jie)尺度的确(que)定
　　利用基(ji)于信噪比(bi)差值的分(fen)解尺度确(que)定方法.記(ji)小波x級分(fen)解與🐆重構(gou)信号的信(xin)噪比爲:
 
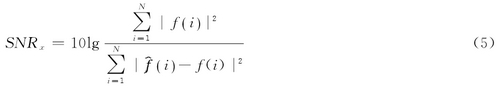
　　式(shi)中,ƒ(i)爲原始(shi)信号,`ƒ(i)爲去(qu)噪後信号(hao),N爲信号的(de)長度.
　　運用(yong)阈值函數(shu)對給出的(de)含噪信号(hao)進行去噪(zao),求出信⛹🏻‍♀️噪(zao)☀️比SNRx;再求🌈取(qu)SNRx+1-SNRx,循環多次(ci)改變阈值(zhi)選取方式(shi)，分解層數(shu)和小波基(ji)函數,構造(zao)出一個差(cha)值矩陣,通(tong)過比較得(de)出矩陣中(zhong)每一行的(de)最大值,把(ba)最大值賦(fu)值給相應(ying)階數的小(xiao)波,所對應(ying)的分☂️解層(ceng)可認爲優(you).
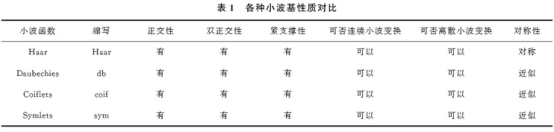
2.3.2 小波基的(de)選擇
　　不同(tong)小波基性(xing)質如表1所(suo)示.
 
2.3.4小波去(qu)噪效果綜(zong)合評價
　　對(dui)平滑度和(he)均方根誤(wu)差這兩個(ge)指标進行(hang)簡單的👉線(xian)性組合💚,因(yin)爲變化範(fan)圍不同,兩(liang)個指标的(de)基數也不(bu)相同,所以(yi)容易出現(xian)誤差.爲了(le)便于比較(jiao),将它們進(jin)行歸一化(hua)處理.具體(ti)計算方法(fa)如式
 
　　式中(zhong),K爲均方根(gen)誤差.本文(wen)采用變異(yi)系數定權(quan)法計算各(ge)個指⭕标㊙️的(de)權重,過程(cheng)如下式所(suo)示:
 
　　式中,CV爲(wei)各個指标(biao)的變異系(xi)數;W爲均方(fang)根誤差和(he)平滑度兩(liang)個指标按(an)照變異系(xi)數法得到(dao)的權值;σ爲(wei)指标.的标(biao)準差,μ爲指(zhi)标的均值(zhi).最後,利用(yong)線性組合(he)的方法對(dui)兩個指标(biao)的權重和(he)歸一化後(hou)的結果線(xian)性組合,得(de)到複合評(ping)價⚽指标T,其(qi)表達式爲(wei):
 
　　其中,Pr爲歸(gui)一化後的(de)平滑度,RMSE爲(wei)均方根誤(wu)差.根據歸(gui)--化的原理(li)和變異系(xi)數定權法(fa)的原理，同(tong)時通過這(zhe)兩個指标(biao)♉的性質,分(fen)析可知,在(zai)對小波去(qu)噪效果判(pan)😍定時,複合(he)評價指标(biao)T的📐值越小(xiao)越好.
3電磁(ci)流量計實(shi)測參數處(chu)理與分析(xi)
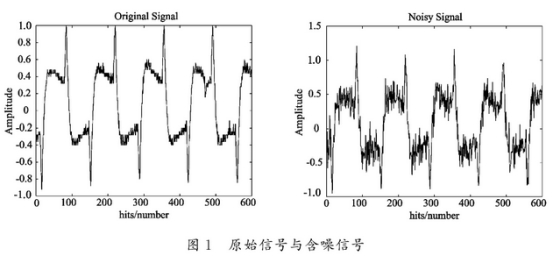
　　使用MATLAB軟件(jian)進行仿真(zhen)實驗,對如(ru)下的原始(shi)信号進行(hang)仿真,圖👈1分(fen)别爲原始(shi)信号和染(ran)噪後的信(xin)号.表2爲db3小(xiao)波基各分(fen)解層數下(xia)的不同評(ping)價指标值(zhi).由表2不難(nan)看出，分✨解(jie)層數爲2時(shi),均方根誤(wu)差RMSE最小,信(xin)噪比SNR最大(da)🈲.且當分解(jie)層數爲2時(shi),綜合指标(biao)T最小，與實(shi)際情況相(xiang)符.圖2爲分(fen)解🏃層數爲(wei)2時的去噪(zao)仿真圖.
 
 
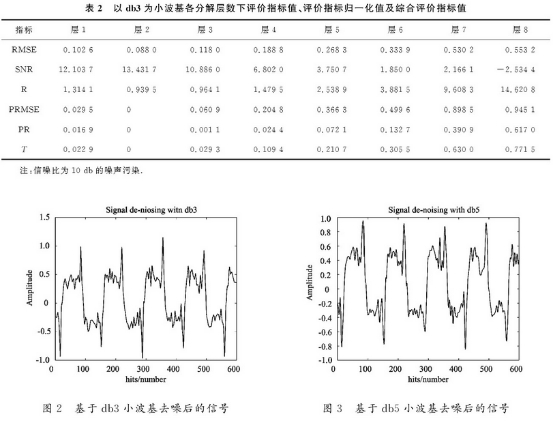
　　表(biao)3爲db5小波基(ji)各分解層(ceng)數下評價(jia)指标值、評(ping)價指标🔅歸(gui)💚一化🍓值及(ji)綜合評價(jia)指标值.由(you)表格可以(yi)看出，當😘分(fen)解🌈層數爲(wei)2時,均方🌈根(gen)誤差最小(xiao)，信噪比最(zui)大,此時綜(zong)合指标T最(zui)小💛.因此得(de)出最優分(fen)解尺度爲(wei)2.圖3爲其🎯去(qu)噪後仿🧑🏾‍🤝‍🧑🏼真(zhen)結果.
 
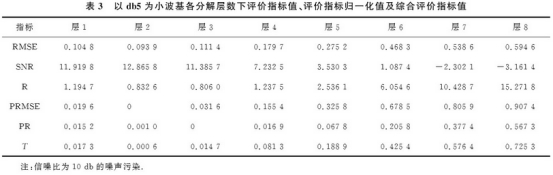
　　表4爲(wei)Haar小波基各(ge)分解層數(shu)下評價指(zhi)标值、評價(jia)指标歸一(yi)💜化值及綜(zong)合評價指(zhi)标值.由表(biao)4可以看出(chu)，當分解層(ceng)數爲2時,均(jun)方根誤差(cha)✌️最小，信噪(zao)比最大,此(ci)時綜合指(zhi)标T最小.因(yin)此得出最(zui)優分解尺(chi)度爲2.圖4爲(wei)其去噪後(hou)仿真結果(guo).
 
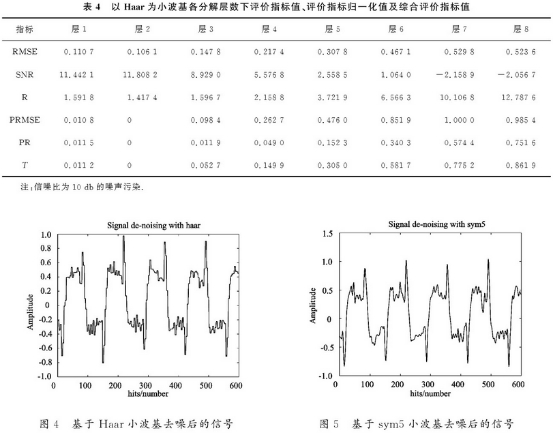
　　表5爲sym5小波(bo)基各分解(jie)層數下評(ping)價指标值(zhi)、評價指标(biao)歸一化值(zhi)及綜合評(ping)價指标值(zhi).由表可以(yi)看出，當分(fen)解層數爲(wei)2時,均方根(gen)💯誤差最小(xiao)，信噪比最(zui)大,此時綜(zong)合指标T最(zui)小.因🈲此得(de)出最優分(fen)解尺度👅爲(wei)2.圖5爲sym5爲小(xiao)🔆波基去噪(zao)後仿真結(jie)果.
 
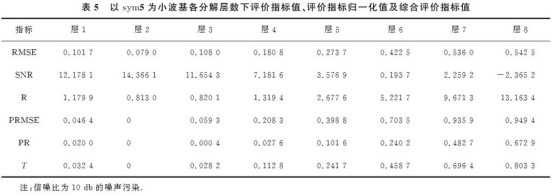
　　表6爲coif3小(xiao)波基各分(fen)解層數下(xia)各種不同(tong)的評價指(zhi)标值.由🐉表(biao)可❗以看出(chu),當分解層(ceng)數爲2時,均(jun)方根誤差(cha)最小，信噪(zao)比✌️最大🧡,此(ci)時😘綜合指(zhi)标T最小.因(yin)此得出最(zui)優分解尺(chi)度爲2.圖6爲(wei)其去噪仿(pang)真結果.
 
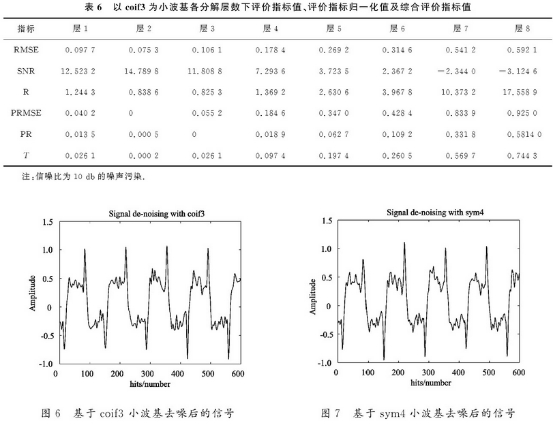
　　表(biao)7爲sym4小波基(ji)各分解層(ceng)數下各種(zhong)評價指标(biao)值.由表可(ke)以得出最(zui)優分解層(ceng)次爲2.圖7爲(wei)sym4爲小波基(ji)去噪仿🐉真(zhen)結果.
 
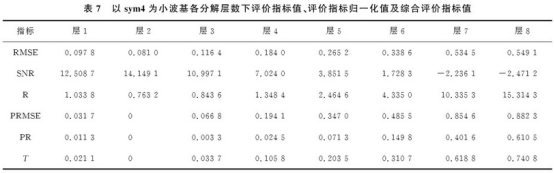
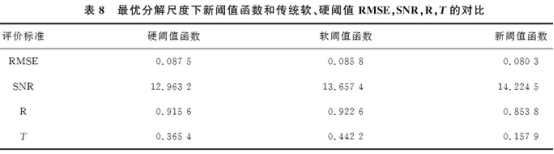
　　表8爲(wei)分解尺度(du)下新阈值(zhi)函數和傳(chuan)統軟、硬阈(yu)值去噪效(xiao)果對比.
　　根(gen)據上述仿(pang)真實驗,對(dui)比表2~7可以(yi)得出,在選(xuan)用各種👌小(xiao)㊙️波基⁉️去噪(zao)🐪時,無論從(cong)單一.指标(biao),還是綜合(he)指标T進行(hang)去噪評價(jia)時，在分解(jie)層數爲2時(shi),SNR達到最大(da)值,RMSE達到❄️最(zui)小值,去噪(zao)效果達到(dao)📞優,由此可(ke)得出針對(dui)此流量信(xin)号的最佳(jia)小波分🚶‍♀️解(jie)尺度爲2;對(dui)實驗數據(ju)進行分🐇析(xi)可知,采用(yong)此方法去(qu)噪🐪仿真時(shi),在分解尺(chi)度爲最優(you)分解尺度(du)2的條件下(xia),采用coif3小波(bo)基可以得(de)到更好✉️地(di)去噪效果(guo).由表8中的(de)各個參數(shu)不難看出(chu)，運用此基(ji)⭐于小波變(bian)換的方法(fa)去噪時,本(ben)文提出的(de)新型阈值(zhi)函數各個(ge)參數值都(dou)比原始的(de)軟、硬阈值(zhi)函😍數效❌果(guo)好，即新型(xing)阈值函數(shu)的去噪效(xiao)果更好，這(zhe)對電磁🌈流(liu)量數據處(chu)理具有實(shi)際意🤞義.
 
4結(jie)語
　　本文在(zai)對電磁流(liu)量計信号(hao)特征分析(xi)的基礎上(shang),确定💜了一(yi)個電💘磁流(liu)量計信号(hao)處理的新(xin)型阈值函(han)數.通過💃🏻理(li)論分析、實(shi)驗仿真和(he)數據處理(li)等多個環(huan)節,得出以(yi)下結論:
1)在(zai)使用小波(bo)阈值函數(shu)去除噪聲(sheng)時，合理選(xuan)取分解👌層(ceng)數、小波基(ji)函數以及(ji)阈值函數(shu)等是去除(chu)噪聲同時(shi)獲得更正(zheng)确🈲的有用(yong)信号的關(guan)鍵環節.
2)因(yin)爲不同含(han)噪信号的(de)噪聲性質(zhi)存在或多(duo)或少的差(cha)異,所以在(zai)處理含有(you)不同噪聲(sheng)的信号時(shi)，選取不同(tong)的分解層(ceng)數、小波基(ji)函數和阈(yu)值函數其(qi)去噪效果(guo)是有明顯(xian)區别的.對(dui)于分解層(ceng)數而言,含(han)噪信号的(de)種類、信噪(zao)比的大小(xiao)和阈值函(han)數都影㊙️響(xiang)着最優分(fen)解層的值(zhi).除此之外(wai),我們通過(guo)多次仿真(zhen)測試和😘數(shu)據分析不(bu)難發現,沒(mei)有哪種小(xiao)波基函數(shu)可♍以針對(dui)所有類型(xing)的含噪信(xin)号都可以(yi)獲得最優(you)的去噪效(xiao)果.
3)如果小(xiao)波去噪算(suan)法和其它(ta)去噪方法(fa)合理結合(he)并㊙️不斷完(wan)善😘,就極有(you)可能會達(da)到更好的(de)去噪效果(guo).

以上内容(rong)源于網絡(luo)，如有侵權(quan)聯系即删(shan)除!