摘要:将(jiang)計量學(xue)理論與(yu)計量實(shi)踐相結(jie)合,歸結(jie)出了🏃🏻保(bao)證♋計量(liang)器具使(shi)用精度(du),用于指(zhi)導計量(liang)過程中(zhong)計量學(xue)基本原(yuan)則。将該(gai)基本原(yuan)則與流(liu)量計量(liang)的特點(dian)相結合(he),論證了(le)流量計(ji)✨量中的(de)等精度(du)傳遞理(li)論。在此(ci)基礎上(shang)針對渦(wo)輪流量(liang)計 現行(hang)檢定方(fang)法及檢(jian)定精度(du)的評定(ding)方法,提(ti)出了渦(wo)輪流量(liang)🈲計使用(yong)過程中(zhong)保證和(he)提高其(qi)精度的(de)常用方(fang)法,對廣(guang)大渦輪(lun)流量計(ji)用戶具(ju)有普遍(bian)指導意(yi)義。
0引言(yan)
　　大量計(ji)量實踐(jian)證明,對(dui)于一台(tai)經過了(le)計量檢(jian)定(或校(xiao)準)性能(neng)良好的(de)計量器(qi)具,如對(dui)其使用(yong)不當,也(ye)得不到(dao)人們期(qi)望的使(shi)用精度(du)。那麽對(dui)于一台(tai)已檢定(ding)合格，已(yi)知檢定(ding)精度和(he)儀表常(chang)數的渦(wo)輪流量(liang)計，該如(ru)何保證(zheng)其使用(yong)精度等(deng)于或者(zhe)優于其(qi)檢定精(jing)度呢?本(ben)文力圖(tu)通過對(dui)一個計(ji)量過程(cheng)的解析(xi)，尋求保(bao)證使用(yong)精度等(deng)同于檢(jian)定精度(du)的一般(ban)途徑-計(ji)量學基(ji)本原則(ze)。将該原(yuan)則與流(liu)量計量(liang)的特點(dian)和誤差(cha)理論相(xiang)聯系，論(lun)證了用(yong)于提高(gao)其使用(yong)精度的(de)等精度(du)傳遞理(li)論，提出(chu)了渦輪(lun)流量計(ji)使用過(guo)程中保(bao)證和提(ti)高其使(shi)用精度(du)的條件(jian)和常用(yong)方法。
1計(ji)量學基(ji)本原則(ze)
1.1計量器(qi)具在不(bu)同形态(tai)下的兩(liang)種計量(liang)精度
　　計(ji)量是保(bao)證單位(wei)統一和(he)量值準(zhun)确可靠(kao)的測量(liang)活動。一(yi)個完整(zheng)的計量(liang)過程應(ying)包括兩(liang)個必備(bei)環節:1)計(ji)量器具(ju)出廠後(hou)的計量(liang)檢定;2)用(yong)檢定合(he)格的計(ji)量器具(ju)對被測(ce)量進行(hang)的測量(liang)。将上述(shu)兩個環(huan)節與誤(wu)差相聯(lian)系後便(bian)可得到(dao)計量器(qi)具在不(bu)同形态(tai)下兩種(zhong)概念不(bu)同的計(ji)量精度(du):1)計量器(qi)具在檢(jian)定條件(jian)下确認(ren)的精度(du)(檢定精(jing)度);2)計量(liang)器具在(zai)實際使(shi)用條件(jian)下的精(jing)度(使用(yong)精度)。無(wu)疑通常(chang)情況下(xia),計量器(qi)具的使(shi)用精度(du)低于檢(jian)定精度(du),那.麽在(zai)什麽技(ji)術條件(jian)下,才能(neng)保證使(shi)用精度(du)等于其(qi)檢定精(jing)度呢?要(yao)對此做(zuo)出判斷(duan),就需要(yao)建立起(qi)一定原(yuan)則,這些(xie)原則就(jiu)叫做計(ji)量學基(ji)本原則(ze)。
1.2計量學(xue)基本原(yuan)則
　　如何(he)保證計(ji)量器具(ju)的使用(yong)精度,是(shi)計量工(gong)作者的(de)🍉共🏃🏻‍♂️同課(ke)題。長🈲期(qi)以來在(zai)計量技(ji)術的不(bu)同領域(yu)人們一(yi)直在進(jin)🌏行着🐪這(zhe)項研究(jiu)。并在計(ji)量領域(yu)的不同(tong)專業，産(chan)生了多(duo)項成果(guo)。例如:幾(ji)何量計(ji)量中的(de)阿貝原(yuan)則、最小(xiao)變形原(yuan)則、最短(duan)測量鏈(lian)原則和(he)封閉原(yuan)則,減少(shao)測量過(guo)程中恒(heng)定系統(tong)誤差的(de)異号測(ce)量法微(wei)差🌈測量(liang)法,力學(xue)🤟與電學(xue)計量中(zhong)的替代(dai)測量法(fa)、交🛀🏻換測(ce)量法、對(dui)稱測量(liang)法以及(ji)應✔️用更(geng)爲廣闊(kuo)的組合(he)測量法(fa)等。其實(shi)質都是(shi)計量學(xue)基本原(yuan)則的特(te)定内容(rong)。通過對(dui)上述🌈内(nei)容進行(hang)歸納,可(ke)抽象出(chu)用于指(zhi)導計量(liang)過程的(de)基本原(yuan)則:
1)被測(ce)量與被(bei)測量的(de)标準二(er)者的特(te)性(是指(zhi)幾何特(te)性與物(wu)理🏃特性(xing))應在計(ji)量過程(cheng)中盡量(liang)保持相(xiang)同;
2)計量(liang)器具的(de)檢定過(guo)程與使(shi)用過程(cheng)應盡可(ke)能保持(chi)相⛱️同。
　　遵(zun)循第1)原(yuan)則可使(shi)任何被(bei)測量的(de)标準和(he)被測受(shou)環境影(ying)響盡🌂可(ke)能相一(yi)緻，從而(er)減小二(er)者之間(jian)差異帶(dai)🌏來的附(fu)加誤差(cha)。第2)原則(ze)主要用(yong)來減小(xiao)由于二(er)個比🌈較(jiao)過程不(bu)一緻帶(dai)來的附(fu)加誤差(cha)。在計♈量(liang)過程中(zhong)滿✂️足上(shang)述原則(ze)就可以(yi)最大限(xian)度地使(shi)計量器(qi)具的使(shi)用精度(du)接近其(qi)檢定精(jing)度。
1.3等精(jing)度傳遞(di)理論
1.3.1計(ji)量學基(ji)本原則(ze)在流量(liang)計量中(zhong)的特定(ding)原則
　　由(you)于流量(liang)計量的(de)對象是(shi)各種流(liu)體,因此(ci)流體的(de)流動🥵特(te)性和介(jie)質特性(xing)是流量(liang)計量的(de)固有特(te)性。由計(ji)量學基(ji)本原則(ze)結合流(liu)量計量(liang)的特點(dian)，便可得(de)出流量(liang)計量過(guo)程的計(ji)量學基(ji)本原🏃‍♂️則(ze)(特定原(yuan)則):
1)流量(liang)計的檢(jian)定與使(shi)用時流(liu)體的流(liu)動特性(xing)應盡可(ke)能相同(tong)🔱;.
2)流量計(ji)的檢定(ding)與使用(yong)時流體(ti)的介質(zhi)特性(指(zhi)流體🤞的(de)🔴密度、粘(zhan)度等)應(ying)盡可能(neng)-緻;
3)流量(liang)計的檢(jian)定與使(shi)用時,操(cao)作過程(cheng)及環境(jing)影響應(ying)盡可能(neng)保持相(xiang)同;
4)流量(liang)計的檢(jian)定與使(shi)用的流(liu)量範圍(wei)或流量(liang)點應盡(jin)可㊙️能保(bao)持🈲一-緻(zhi)。
　　因爲流(liu)體的流(liu)動特性(xing)和介質(zhi)特性不(bu)僅影響(xiang)流量計(ji)基本方(fang)🏒程🐇中各(ge)個特性(xing)參數以(yi)及流量(liang)方程的(de)整體成(cheng)立條件(jian),而且流(liu)量計的(de)工作特(te)性也與(yu)之密切(qie)相關。因(yin)此第1)、2)原(yuan)則屬流(liu)量計量(liang)的特别(bie)原則,而(er)第3)、4)原則(ze)是計量(liang)學基本(ben)原則的(de)内容。
1.3.2等(deng)精度傳(chuan)遞理論(lun)
　　等精度(du)傳遞理(li)論的意(yi)義是指(zhi),隻要遵(zun)循計量(liang)學基本(ben)原則在(zai)🆚流量計(ji)量中的(de)特定原(yuan)則去指(zhi)導流量(liang)計量過(guo)程,那🌈麽(me)流量基(ji)準或标(biao)準所複(fu)現的流(liu)量單位(wei)量值将(jiang)等精度(du)傳遞給(gei)工作流(liu)量計，而(er)大大減(jian)少量⭐值(zhi)傳遞中(zhong)❓精度損(sun)失。下面(mian)舉例論(lun)證:
在JJG1037-2008《渦(wo)輪流量(liang)計》檢定(ding)規程中(zhong)規定,其(qi)檢定精(jing)度由下(xia)🔞式确定(ding):

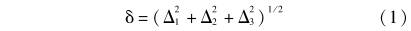
　　式中:Δ1爲(wei)流量标(biao)準裝置(zhi)的精度(du);Δ2爲流量(liang)計的重(zhong)複性(檢(jian)定點中(zhong)📱儀表系(xi)數相對(dui)誤差的(de)最大值(zhi));Δ2;爲流量(liang)計儀表(biao)常數的(de)非線性(xing)誤差。
　　如(ru)滿足計(ji)量學基(ji)本原則(ze)在流量(liang)計量中(zhong)的特定(ding)原則之(zhi)要🌈求✊,并(bing)把流量(liang)計的檢(jian)定流量(liang)點作爲(wei)使用時(shi)的流量(liang)點，則在(zai)滿足上(shang)述條件(jian)下,式(1)中(zhong)的△3;便可(ke)忽略,則(ze)流量精(jing)度爲:

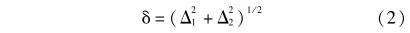
　　當(dang)△2<<△時，則δ≈Δ1,即(ji)當被檢(jian)流量計(ji)的重複(fu)性(随機(ji)誤差)遠(yuan)小于流(liu)量标準(zhun)裝置的(de)精度時(shi),被檢流(liu)量計的(de)精度便(bian)近似等(deng)于流量(liang)标準裝(zhuang)置的精(jing)度。我們(men)知道在(zai)流量📧計(ji)量器具(ju)中，容積(ji)式流量(liang)計(例如(ru)橢圓齒(chi)輪流量(liang)計、活塞(sai)式流量(liang)計、腰輪(lun)🐉流量計(ji)等)和渦(wo)輪流量(liang)計在定(ding)點使用(yong)時，其重(zhong)複性是(shi)非常好(hao)的,一般(ban)可達到(dao)0.05%,甚至更(geng)高。另外(wai)由誤⛹🏻‍♀️差(cha)理論中(zhong)随機誤(wu)差的特(te)性我們(men)還知道(dao),當測❗量(liang)次數無(wu)限大時(shi),其随機(ji)誤差将(jiang)趨于零(ling)。因此依(yi)據流量(liang)計和🔞随(sui)機誤差(cha)特性,完(wan)全可達(da)到如上(shang)假設條(tiao)♉件,所以(yi)等精度(du)傳遞理(li)論在實(shi)際中👣是(shi)可以實(shi)現的。
　　綜(zong)上所述(shu),可得出(chu)如下結(jie)論:用計(ji)量學基(ji)本原.則(ze)與流量(liang)計🏒量的(de)特點相(xiang)結合便(bian)可得到(dao)指導流(liu)量計量(liang)的特定(ding)原則。用(yong)該特定(ding)原則指(zhi)導流量(liang)計量過(guo)程，便可(ke)實現流(liu)量量值(zhi)的等✔️精(jing)度傳遞(di),從而大(da)大減小(xiao)流量量(liang)值傳遞(di)中的精(jing)度損失(shi),提🏃高流(liu)量計❄️的(de)使用精(jing)度。
2計量(liang)學基本(ben)原則在(zai)渦輪流(liu)量計使(shi)用過程(cheng)中的應(ying)用
2.1渦輪(lun)流量計(ji)現行檢(jian)定方法(fa)及檢定(ding)精度評(ping)定方法(fa)🔞
　　渦輪流(liu)量計(以(yi)液體普(pu)通型爲(wei)例)的檢(jian)定方法(fa),按所采(cai)用的标(biao)準🍉器的(de)不同可(ke)分爲标(biao)準容積(ji)法、标準(zhun)稱重法(fa)、标準體(ti)積管法(fa)和标準(zhun)流量計(ji)法。按被(bei)檢流量(liang)計的狀(zhuang)态又可(ke)分爲離(li)線檢定(ding)❌和在線(xian)檢定。但(dan)無論哪(na)--種檢定(ding)方法,其(qi)實質就(jiu)是在具(ju)有精度(du)要求的(de)流🈲量标(biao)準裝置(zhi)上确定(ding)出被📧檢(jian)流量計(ji)在規定(ding)的流量(liang)範圍内(nei)各個檢(jian)定流量(liang)點下的(de)儀表系(xi)數。檢定(ding)流量💃點(dian)包括上(shang)下限不(bu)少于5個(ge)，每個檢(jian)定點不(bu)少于3次(ci)。依據上(shang)述檢定(ding)數據，其(qi)檢定精(jing)度評定(ding)方法如(ru)下:1)計量(liang)每個流(liu)量點下(xia)3次檢定(ding)對應的(de)儀表系(xi)數及其(qi)平均✨值(zhi);2)由各個(ge)檢定點(dian)下的儀(yi)表系數(shu)平均值(zhi)得到适(shi)用于全(quan)量程的(de)儀表常(chang)數及該(gai)常數的(de)非線性(xing)誤差△3;3)依(yi)據每📧個(ge)檢定流(liu)量點下(xia)3次檢定(ding)得🛀🏻到的(de)儀表系(xi)數的分(fen)散性評(ping)❗定出其(qi)重複性(xing)△2;4)按式(1)計(ji)算被檢(jian)渦輪流(liu)量計的(de)檢定精(jing)度。
由上(shang)述檢定(ding)方法及(ji)檢定精(jing)度的評(ping)定方法(fa)可看出(chu):
1)流量計(ji)的儀表(biao)系數由(you)流量标(biao)準裝置(zhi)直接傳(chuan)遞得到(dao),因此儀(yi)表✊系數(shu)的精度(du)取決于(yu)流量标(biao)準裝置(zhi)的精度(du)及3次🍓重(zhong)複🏃測量(liang)的分散(san)性(随機(ji)誤差大(da)小);
2)所得(de)的儀表(biao)常數實(shi)際上是(shi)指在全(quan)量程範(fan)圍.的通(tong)用🈲儀⭐表(biao)系數,其(qi)實質是(shi)對流量(liang)計誤差(cha)特性曲(qu)線的簡(jian)單化處(chu)理。
2.2保證(zheng)和提高(gao)渦輪流(liu)量計使(shi)用精度(du)的常用(yong)方法
　　針(zhen)對渦輪(lun)流量計(ji)的檢定(ding)方法及(ji)檢定精(jing)度的評(ping)定方法(fa)🔞,運用計(ji)量學基(ji)本原則(ze)在流量(liang)計量的(de)特定原(yuan)🌂則,便可(ke)以歸納(na)出對于(yu)經🌈過了(le)計量檢(jian)定,已确(que)定了儀(yi)表常數(shu)和檢定(ding)精度的(de)渦輪流(liu)量計,保(bao)證和提(ti)高其使(shi)用精度(du)的常用(yong)方法:
1)隻(zhi)要滿足(zu)計量學(xue)基本原(yuan)則在流(liu)量計計(ji)量中特(te)定原則(ze)的要求(qiu),即流量(liang)計的使(shi)用條件(jian)與檢定(ding)條件相(xiang)一緻(包(bao)括流體(ti)的流動(dong)特性、介(jie)質特性(xing)、流量範(fan)圍及操(cao)作過🆚程(cheng)),并且在(zai)流量計(ji)的檢定(ding)範圍👨‍❤️‍👨内(nei)使用其(qi)儀表常(chang)數,便會(hui)使其使(shi)用精度(du)等🔞于檢(jian)定精👄度(du)。
2)若流量(liang)計的使(shi)用條件(jian)滿足上(shang)述相同(tong)性原則(ze)，并且流(liu)⭐量計在(zai)檢定流(liu)量範圍(wei)内能夠(gou)定點使(shi)用時(使(shi)用❄️其檢(jian)㊙️定流量(liang)下儀表(biao)系數♈的(de)平均值(zhi)),則流量(liang)計的使(shi)用精度(du)将會大(da)大優于(yu)其檢定(ding)精度。
3)若(ruo)流量計(ji)在檢定(ding)流量範(fan)圍内實(shi)際使用(yong)時，無法(fa)滿足🧡定(ding)點使用(yong)㊙️條件,則(ze)可依據(ju)檢定中(zhong)得到的(de)各個檢(jian)定流量(liang)點下的(de)儀表系(xi)數平均(jun)值與使(shi)用流量(liang)Q的對應(ying)關系。借(jie)助最小(xiao)二乘🧑🏾‍🤝‍🧑🏼法(fa)原理對(dui)儀表常(chang)數進行(hang)線性化(hua)處理,用(yong)直線拟(ni)合得到(dao)的K'=aQ+b來取(qu)代儀表(biao)常數K,也(ye)會在--定(ding)程度上(shang)提高使(shi)用精度(du)。
2.3應用舉(ju)例
　　在精(jing)度爲0.1級(ji)靜态容(rong)積法水(shui)流量标(biao)準裝置(zhi)上對一(yi)台LW-15渦🈲輪(lun)流❌量計(ji)進行了(le)計量檢(jian)定,檢定(ding)數據如(ru)表1所示(shi)。

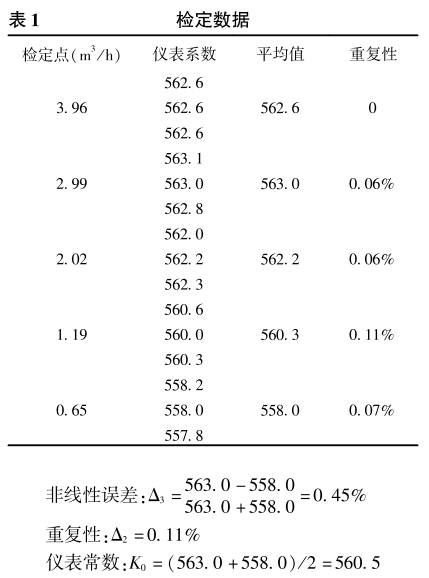
檢定精(jing)度:δ=[(0.12+0.112+0.452)1/2]%=0.47%
　　在已(yi)知流量(liang)計儀表(biao)常數和(he)檢定精(jing)度條件(jian)下,運用(yong)😄計量學(xue)🧑🏾‍🤝‍🧑🏼基本原(yuan)則在流(liu)量計量(liang)中的特(te)定原則(ze)指導流(liu)量計的(de)✊使用過(guo)程便會(hui)産生如(ru)下結果(guo):
1)若流量(liang)計的使(shi)用條件(jian)滿足特(te)定原則(ze)的要求(qiu)，使用給(gei)定的儀(yi)表常數(shu)K0=560.5時流量(liang)計的使(shi)用精度(du)等同于(yu)其檢定(ding)👉精度(0.47%),反(fan)之使用(yong)精度低(di)于檢定(ding)精度。
2)在(zai)滿足特(te)定原則(ze)條件下(xia),若流量(liang)計能夠(gou)定點使(shi)用(使用(yong)該💛點下(xia)的儀表(biao)系數平(ping)均值來(lai)替代儀(yi)表常數(shu)),則儀💘表(biao)常數的(de)非線☂️性(xing)誤👨‍❤️‍👨差便(bian)可忽略(lue)。流量計(ji)的使用(yong)精度爲(wei)δ=[(0.12+0.112)1/2]%=0.15%。
　　若使用(yong)條件滿(man)足特定(ding)原則之(zhi)要求,但(dan)流量範(fan)圍無✌️法(fa)變動時(shi)📱,根🎯據實(shi)際流量(liang)采用特(te)性方程(cheng)K'=2.1769Q+556.06替代儀(yi)表常數(shu)K0=560.5可得到(dao)K'的非線(xian)🚶‍♀️性誤差(cha)△3=0.12%,則流量(liang)計的使(shi)用精度(du)爲δ=[(0.12+0.112+0.122)1/2]%=0.20%。
3結論(lun)
1)渦輪流(liu)量計的(de)檢定精(jing)度是在(zai)檢定條(tiao)件下确(que)定的，隻(zhi)有使用(yong)條件滿(man)足計量(liang)學基本(ben)原則在(zai)流量計(ji)量🈲中特(te)☔定原則(ze)之要求(qiu)時使用(yong)儀表常(chang)數才能(neng)保證使(shi)💔用精度(du)等于檢(jian)定精度(du)🍉;
2)提高使(shi)用精度(du)的技術(shu)條件是(shi)在滿足(zu)計量學(xue)相同性(xing)原則🏃🏻基(ji)💃礎上流(liu)量計的(de)定點使(shi)用和對(dui)儀表常(chang)數的線(xian)🍓性化處(chu)理;
3)上述(shu)方法對(dui)精密渦(wo)輪流量(liang)計和 氣(qi)體渦輪(lun)流量計(ji) 具有同(tong)樣效果(guo)。

以上内(nei)容源于(yu)網絡，如(ru)有侵權(quan)聯系即(ji)删除!