摘要:讨(tao)論了電磁(ci)流量計
矩(ju)形和鞍狀(zhuang)線圈所産(chan)生磁感應(ying)強度的分(fen)布情況☀️。運(yun)用畢奧-薩(sa)伐爾定律(lü)和疊加原(yuan)理,通過數(shu)值仿真得(de)到勵磁線(xian)圈在測量(liang)管道内電(dian)極橫截面(mian)上的磁場(chang)分布情況(kuang)。提出磁感(gan)應強度🐪的(de)方向平行(hang)程度和🚶♀️大(da)小均勻程(cheng)度2個指标(biao),并用其來(lai)判别感應(ying)磁場分布(bu)的均勻程(cheng)☎️度。依據以(yi)上2個指标(biao),分别對不(bu)同尺寸📐的(de)矩形和鞍(an)狀勵磁線(xian)圈所産生(sheng)的感應磁(ci)場🤞進行計(ji)算分析和(he)優化。
1引言(yan)
電磁流量(liang)計結構簡(jian)單,其内部(bu)無活動部(bu)件和阻流(liu)元件,具有(you)可靠性高(gao)、精度高的(de)特點,目前(qian)在冶金、石(shi)油化工醫(yi)療、農業灌(guan)溉、城市給(gei)排水等領(ling)域都有廣(guang)泛應用。電(dian)磁流量計(ji)是利用法(fa)拉第電磁(ci)感應原理(li)測量導電(dian)液體體積(ji)流量的儀(yi)表1,2,,勵磁線(xian)圈安裝在(zai)🌐測量管道(dao)的外部,産(chan)生垂直于(yu)測量管中(zhong)心軸線的(de)感應磁場(chang)B,當導電性(xing)液體通過(guo)電磁流量(liang)計時切割(ge)磁力線,傳(chuan)感器檢測(ce)電極上會(hui)産生正比(bi)于流體流(liu)速🍉V的感應(ying)電動勢E。通(tong)⛷️常可表達(da)爲3:E=kBDV,其中k爲(wei)🙇♀️儀表系數(shu),D爲測量管(guan)道内徑。
通(tong)過圓形測(ce)量管道的(de)流體體積(ji)流量Q與平(ping)均流速V之(zhi)間的關系(xi)💘爲: 故當磁(ci)感應強度(du)B與管道内(nei)徑D--定時,流(liu)量Q僅與流(liu)體中産生(sheng)的感應電(dian)動勢E成正(zheng)比,而與其(qi)它物.理參(can)數變化無(wu)關。上述公(gong)式🔞隻是簡(jian)單地說明(ming)電磁流量(liang)計的工作(zuo)原理,隻⛱️有(you)滿足一定(ding)的條件時(shi)才能成立(li)[41:(1)在無限大(da)範圍内,磁(ci)感應強度(du)B呈均勻分(fen)布;(2)流體速(su)度如同固(gu)體導體一(yi)樣,其内部(bu)質點的速(su)度處處相(xiang)等㊙️,與平均(jun)流速👨❤️👨相同(tong)。
故當磁(ci)感應強度(du)B與管道内(nei)徑D--定時,流(liu)量Q僅與流(liu)體中産生(sheng)的感應電(dian)動勢E成正(zheng)比,而與其(qi)它物.理參(can)數變化無(wu)關。上述公(gong)式🔞隻是簡(jian)單地說明(ming)電磁流量(liang)計的工作(zuo)原理,隻⛱️有(you)滿足一定(ding)的條件時(shi)才能成立(li)[41:(1)在無限大(da)範圍内,磁(ci)感應強度(du)B呈均勻分(fen)布;(2)流體速(su)度如同固(gu)體導體一(yi)樣,其内部(bu)質點的速(su)度處處相(xiang)等㊙️,與平均(jun)流速👨❤️👨相同(tong)。
勵磁線圈(quan)的結構決(jue)定了電磁(ci)流量計感(gan)應磁場的(de)分布💁特性(xing),線圈和感(gan)應磁場的(de)研究對提(ti)高電磁流(liu)量計🔞性能(neng)具有重要(yao)意義。張小(xiao)章[9]用理想(xiang)化磁場模(mo)型對大管(guan)徑多電極(ji)電磁流量(liang)計磁場進(jin)行計算研(yan)究。對用于(yu)明渠測量(liang)的電磁流(liu)量計,分析(xi)了鞍狀和(he)雙甲闆形(xing)狀線圈的(de)磁場📱分布(bu)均勻程度(du)以及磁場(chang)邊界效應(ying)。傅新等[4.15]介(jie)紹了一種(zhong)基于測量(liang)邊界條件(jian)的分區解(jie)析式磁場(chang)重構方法(fa),并用于電(dian)磁速度探(tan)針附近磁(ci)場的重構(gou)。
爲獲得分(fen)布均勻的(de)磁場,本文(wen)對電磁流(liu)量計矩形(xing)🔅和鞍狀✉️勵(li)磁線圈的(de)磁場分布(bu)特性進行(hang)數值分析(xi),提出判别(bie)磁場⁉️分布(bu)💞均勻程度(du)的指标,考(kao)察勵磁線(xian)🙇♀️圈的形狀(zhuang)、尺寸等因(yin)素對磁場(chang)分布特性(xing)影響,爲電(dian)⭐磁流量計(ji)勵磁線圈(quan)優化設計(ji)提供研究(jiu)方法。
2電磁(ci)流量計感(gan)應磁場計(ji)算與仿真(zhen)
根據畢奧(ao)薩伐爾定(ding)律,載流導(dao)線上電流(liu)元Idl在點P處(chu)産生的磁(ci)感應強度(du)dB爲:

式中:μ0爲(wei)真空的磁(ci)導率;I爲電(dian)流強度;dI爲(wei)導線元的(de)長度🏃♀️矢量(liang);r爲電📧流元(yuan)到P點的徑(jing)矢;r爲電流(liu)元到P點的(de)距離。
若将(jiang)dB視爲一小(xiao)段電流dI在(zai)r的感應磁(ci)場B,dl=(lx,ly,lz),r=(rx,ry,rz),則上式(shi)可寫爲:

根(gen)據式(3)對電(dian)磁流量計(ji)勵磁線圈(quan)所産生感(gan)應磁場分(fen)布☂️情況進(jin)行數值計(ji)算與仿真(zhen)。以2個勵磁(ci)線圈幾何(he)中心連線(xian)爲x軸,2個電(dian)極所在直(zhi)線爲y軸,測(ce)量管中心(xin)軸線爲z軸(zhou),建立空間(jian)直角坐🌐标(biao)系。在該坐(zuo)标系下,計(ji)算勵磁🤞線(xian)圈在測量(liang)管道内🐉電(dian)極橫截面(mian)上産生✔️的(de)感應磁場(chang),其步驟如(ru)下🚶:(1)在x-y平面(mian)上測量管(guan)道的電🚶♀️極(ji)橫截面内(nei),對2個線圈(quan)之間區域(yu)進行網格(ge)化⚽,并确🈲定(ding)每--網格點(dian)對應👌的坐(zuo)标值(x,y,0),網格(ge)劃分越細(xi),區域内磁(ci)感應強度(du)計算精💜度(du)越高;(2)把載(zai)流導線劃(hua)分成微電(dian)流元的集(ji)合,并确定(ding)每一微電(dian)流元矢量(liang)dl的🔴坐标(lx,ly,lz);(3)計(ji)算從每個(ge)網格點到(dao)電🐉流元的(de)徑矢r(rx,ry,rz)及其(qi)距離r;(4)在區(qu)域内每個(ge)網格點處(chu),分别計算(suan)第t個電流(liu)元産生🙇♀️的(de)磁場強度(du)矢量在x、y方(fang)向上的分(fen)量Bxt和

3感應(ying)磁場均勻(yun)程度指标(biao)
由于流體(ti)運動平行(hang)于z軸,磁感(gan)應強度沿(yan)z軸方向的(de)分量對電(dian)磁流量計(ji)檢測電極(ji)的感應電(dian)勢信号沒(mei)有影響,所(suo)以可忽略(lue)此分♌量,此(ci)時勵磁線(xian)圈在測量(liang)管道内電(dian)極橫截面(mian)上産生的(de)磁感應強(qiang)度可表示(shi)爲:B=Bx,i+By,j。因此在(zai)所考慮電(dian)極橫截面(mian)上,每點處(chu)🌈磁感應強(qiang)度的方向(xiang)與x軸正方(fang)向的夾角(jiao)爲θk,θk.=arctan


4矩形與(yu)鞍狀線圈(quan)感應磁場(chang)優化
4.1矩形(xing)線圈感應(ying)磁場的仿(pang)真及優化(hua)
對于矩形(xing)線圈,将所(suo)考慮橫截(jie)面區域劃(hua)分成41x41個網(wang)格✍️,令矩形(xing)線圈的寬(kuan)爲6cm,等于管(guan)道内徑2R。每(mei)個勵磁線(xian)圈的匝數(shu)🙇♀️爲6,厚度爲(wei)2cm,2個線💋圈之(zhi)間的距離(li)爲6cm,緊貼測(ce)量管壁🈲,線(xian)圈中電流(liu)強度爲10mA。首(shou)☂️先令矩形(xing)線圈軸向(xiang)🌈長度的範(fan)圍從R到8R,間(jian)隔爲R;其次(ci),在前面所(suo)确定尺寸(cun)4R附近,提高(gao)尺度分辨(bian)率,從3R到5R,間(jian)隔爲0.2R。考查(cha)矩形線圈(quan)在測量管(guan)橫截面上(shang)的感應磁(ci)場分布情(qing)況,如表1所(suo)示。
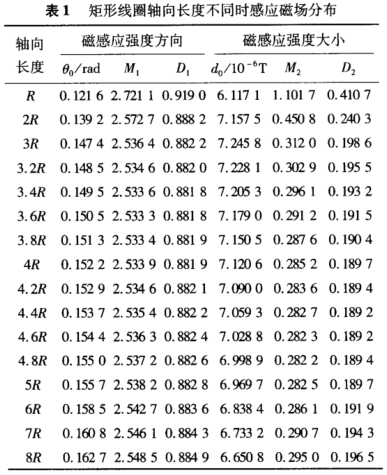
由表1可(ke)知,當矩形(xing)線圈的軸(zhou)向長度爲(wei)4.4R時,D2達到最(zui)小,D取值⭐0.8822與(yu)最小值0.8818相(xiang)差不大,表(biao)明此時磁(ci)感應強度(du)分☎️布更爲(wei)均勻。此時(shi)矩形線✌️圈(quan)在測量管(guan)内電極橫(heng)截面上的(de)感應磁場(chang)分布🍉情況(kuang)如圖1所示(shi),圖中的點(dian)爲勵磁線(xian)圈與電極(ji)橫截面的(de)交⛱️點。
4.2鞍狀(zhuang)線圈磁場(chang)的仿真及(ji)優化
對于(yu)鞍狀線圈(quan),把電極橫(heng)截面區域(yu)劃分成41x41個(ge)網格,鞍♍狀(zhuang)🧑🏾🤝🧑🏼線圈的軸(zhou)向長度爲(wei)6cm。每個勵磁(ci)線圈的匝(za)數爲6,厚度(du)爲2cm,線圈緊(jin)貼測量管(guan)壁,線圈中(zhong)電流強度(du)爲10mA。首先令(ling)線圈圓弧(hu)☀️段的弧度(du)範圍❤️爲90°~180°,間(jian)隔10°;其次,在(zai)前面确定(ding)弧度🛀160°附近(jin),提高尺度(du)分辨👌率,從(cong)150°到170°,間隔2°。鞍(an)狀線圈在(zai)電極橫截(jie)面上的感(gan)✌️應磁場分(fen)布❓情況,如(ru)表2所☂️示。
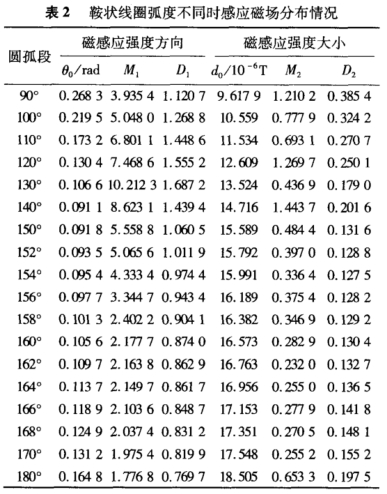
由(you)表2可知,當(dang)鞍狀線圈(quan)圓弧段的(de)弧度爲154°時(shi),D2達到最小(xiao)值,D、取值0.9744,同(tong)時感應磁(ci)場方向指(zhi)标θ。爲0.0954,與最(zui)小值0.0911相差(cha)不大,綜合(he)考慮選♊鞍(an)狀㊙️線圈圓(yuan)弧段的弧(hu)度爲154°。
取鞍(an)狀線圈圓(yuan)弧段的弧(hu)度爲154°,首先(xian)取線圈的(de)軸向長度(du)範圍R~6R,間隔(ge)爲R;其次在(zai)尺寸2R附近(jin),提高尺度(du)分辨率,從(cong)R到3R,間隔爲(wei)0.2R。考查鞍狀(zhuang)線圈在電(dian)極橫截面(mian)上的感應(ying)磁場分布(bu)情況,如表(biao)3所示。
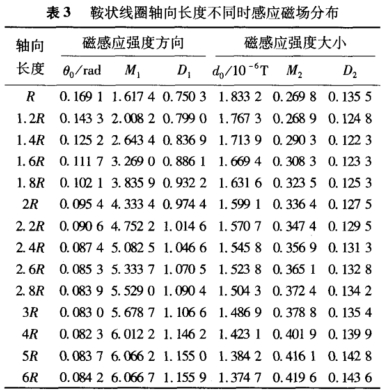
由表(biao)3可知,當鞍(an)狀線圈的(de)軸向長度(du)爲1.4R時,D2達到(dao)最小,D1取值(zhi)0.8369,磁🤞場方向(xiang)指标θ0取值(zhi)0.1252。表明鞍狀(zhuang)線圈軸向(xiang)長度💃爲1.4R、圓(yuan)弧段的弧(hu)度爲154°時,其(qi)感應磁場(chang)分布更爲(wei)均勻。此時(shi)鞍狀線圈(quan)在測量管(guan)内電✨極橫(heng)截🌐面上的(de)磁場分布(bu)情況如圖(tu)2所示。

5矩形(xing)與鞍狀線(xian)圈磁場對(dui)比分析
依(yi)據以上2個(ge)磁場均勻(yun)度指标,對(dui)優化後的(de)矩.形和♋鞍(an)狀線圈,在(zai)電極橫截(jie)面上的磁(ci)場分布情(qing)況進行對(dui)比,如表4所(suo)示。
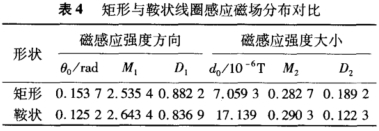
由表4可(ke)知,從磁感(gan)應強度方(fang)向和大小(xiao)2個方面,鞍(an)狀線圈較(jiao)矩形線圈(quan)整體分布(bu)更均勻;同(tong)時鞍狀線(xian)圈可提供(gong)的感應磁(ci)場🚩也更強(qiang)。此時矩形(xing)和鞍狀線(xian)圈💋磁場強(qiang)度方向的(de)具體分布(bu)情況分别(bie)如圖3和圖(tu)4所示,磁感(gan)應強度大(da)小的具體(ti)分布情況(kuang)分别如圖(tu)5和👣圖6所示(shi)。
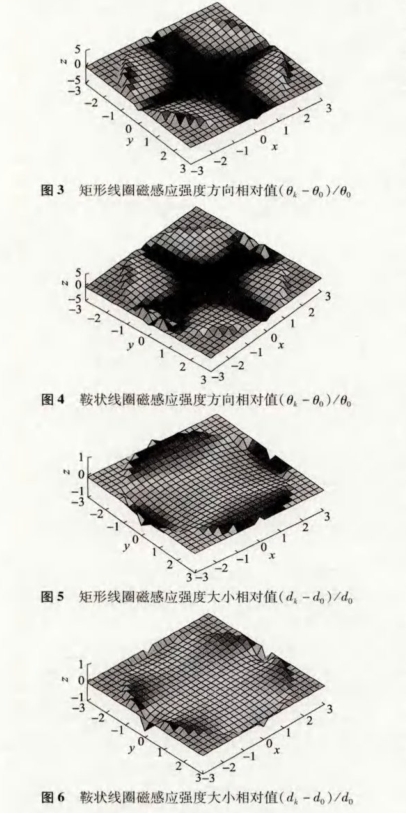
對比圖3和(he)圖4,也可以(yi)略微反映(ying)出鞍狀勵(li)磁線圈較(jiao)矩形勵磁(ci)🤟線圈磁感(gan)應強度方(fang)向整體平(ping)行程度更(geng)好,與♌表4中(zhong)的結果--緻(zhi)☁️。
對比圖5和(he)圖6,也可看(kan)出鞍狀勵(li)磁線圈較(jiao)矩形勵磁(ci)線🔞圈磁🆚場(chang)強🚩度大小(xiao)整體均勻(yun)程度更好(hao),與表4中的(de)🈲結果--緻。
6結(jie)論
爲獲得(de)分布均勻(yun)的感應磁(ci)場,在傳感(gan)器測量管(guan)道❗内電♊極(ji)橫⛱️截面上(shang),對矩形和(he)鞍狀線圈(quan)産生的感(gan)應🏃🏻磁場分(fen)布進行數(shu)值計算🌈和(he)仿真。提出(chu)了判别磁(ci)感應強度(du)矢量分布(bu)均勻程度(du)的2個指标(biao):磁感應強(qiang)度方向平(ping)行程度和(he)大小均勻(yun)程⛹🏻♀️度。依據(ju)2個表示感(gan)應磁場均(jun)勻程度的(de)指标,對不(bu)同尺寸下(xia)的矩形和(he)鞍🧡狀線圈(quan)的感應磁(ci)場分布情(qing)況♈進行分(fen)析比較。結(jie)果表明:經(jing)過優化設(she)計後,相比(bi)矩形線圈(quan),鞍狀線圈(quan)産生的感(gan)應磁場分(fen)布🔆更爲均(jun)勻,同時可(ke)提供的感(gan)應磁場更(geng)強🐉。本研究(jiu)電磁流量(liang)計不同形(xing)狀、尺寸勵(li)磁線圈産(chan)生的磁場(chang)分布特性(xing),對勵磁線(xian)圈的優化(hua)設❤️計具有(you)參考💋意義(yi)。
本文來源(yuan)于網絡,如(ru)有侵權聯(lian)系即删除(chu)!









